Tidal Thruster: A Tidal Force Analogy for Asymmetrical Capacitor Propulsion

Dr. Bühler’s Asymmetrical Capacitor Drive and the Equivalence Principle

Dr. Bühler’s asymmetrical capacitor drive presents an intriguing phenomenon: when an asymmetrical capacitor is charged, it experiences a net force in the direction of the smaller electrode. This force emerges due to the interaction of electrostatic pressure gradients within the dielectric material. Interestingly, we can compare this effect to the behavior of a dielectric rod suspended in a gravitational field, revealing deep connections between electrostatic forces and the equivalence principle.

The asymmetrical capacitor drive proposed by Dr. Bühler exhibits a net force toward the smaller capacitor plate, a phenomenon that we argue is deeply connected to the equivalence principle and gravitational tidal effects in dielectrics. If a dielectric rod is suspended in a gravitational field, it undergoes internal stresses similar to those seen in an asymmetrical capacitor, suggesting a fundamental link between space curvature, electric fields, and material deformations.

While this remains a speculative hypothesis, this is my personal attempt to understand the phenomenon—if the phenomenon is real—and to offer a possible theoretical framework to interpret it.

Tidal Forces in a Dielectric Rod

A dielectric rod, when placed in a gravitational field, experiences tidal forces. These forces induce an internal stress distribution, leading to elongation along its longer axis, localized radial contraction at one end, and the emergence of an electric field within the dielectric. The internal polarization results from gravitationally induced strain, leading to charge redistribution and a corresponding internal electric field. This deformation and field generation provide a striking parallel to the behavior of an asymmetrical capacitor.

Asymmetrical Capacitor and Dielectric Response

In an asymmetrical capacitor, the electric field is unevenly distributed due to the different electrode sizes. The dielectric experiences internal stresses, leading to a net force toward the smaller plate. This phenomenon arises from a non-uniform electrostatic pressure distribution within the dielectric, mirroring the effect of gravitational tidal forces on the dielectric rod.

The Equivalence Principle in Action

If we enclose both systems—(1) the dielectric rod in a gravitational field and (2) the asymmetrical capacitor—in separate black boxes, an observer within each box would detect strikingly similar effects:

• Internal stresses within the dielectric.

• Elongation along the primary axis.

• An induced internal electric field.

• A tendency for one end to shrink radially.

This equivalence suggests that the net force observed in the asymmetrical capacitor may be understood as an electrostatic analogue of gravitational tidal forces. The interplay between charge distribution, field-induced stresses, and internal polarization aligns with the way matter responds to spacetime curvature under gravitational influence.

Since both scenarios produce the same effects, the equivalence principle suggests that if space curvature induces asymmetrical dielectric deformations, then dielectric deformations must, in turn, induce space curvature.

1. Tidal Forces in a Dielectric Rod in a Gravitational Field

Consider a dielectric rod of length L, mass density ρ, and permittivity ϵ, suspended in a gravitational field g. Due to the tidal nature of gravity, the ends of the rod experience slightly different gravitational accelerations, producing a tidal acceleration across the length of the rod:

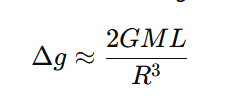
where M is the mass of the planet, and R is the distance to its center. This induces a tidal stress:

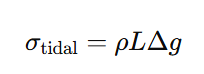
which generates an internal electric field due to charge polarization effects in the dielectric:

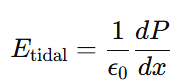
At the same time, geodesic motion leads to a radial contraction at one end of the rod, as space-time curvature naturally directs part of the material inward toward the planet’s core. The contraction is described by:

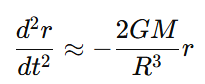
2. Asymmetrical Capacitor: Induced Stress and the Equivalence Principle

In an asymmetrical capacitor, a strong electric field EEE is applied between two plates, one large and one small, with a dielectric in between. The electric pressure is stronger near the smaller plate, leading to an asymmetric electrostatic force distribution. The force per unit area is given by:

which results in an internal electrostatic stress:

Since the smaller plate has higher field strength, the dielectric experiences asymmetric stretching in the same manner as in the gravitational case. However, unlike the gravitational system where geodesic motion naturally causes the contraction at one end, in the capacitor system, we must manually shape the smaller plate to induce this effect.

3. Matching Gravitational and Electrostatic Deformations

Since both systems exhibit the same stretching and internal field effects, the equivalence principle suggests that if space curvature induces asymmetrical deformations in dielectrics, then dielectric deformations should, in turn, induce space curvature.

To explore this further, we propose the following experimental hypothesis:

• If we shape the asymmetrical capacitor’s dielectric to match the gravitational deformations of the rod under a given gravitational field g,

• And if we apply an electric current or charge distribution that scales according to some factor k,

• Then the capacitor system should exhibit the same effective acceleration as the gravitational system, leading to motion.

This means that, using General Relativity formulas, we should be able to determine the proper dielectric shape and charge distribution to obtain a force equivalent to gravitational free fall with acceleration g.

4. A Dependency Formula Between Dielectric Deformation and Space Curvature

If tidal stress σ​ in a dielectric is linked to curvature Rμν, then, reciprocally, an applied stress σ should generate an equivalent curvature. We propose the relation:

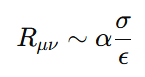
5.Doped Dielectrics and Induced Electric Stresses

By doping the dielectric with specific elements, such as nitrogen in carbon-based materials, it’s possible to enhance the material’s response to electromagnetic radiation. This doping can lead to the induction of internal dipoles that increase the dielectric’s polarization when exposed to external electromagnetic fields. The doped dielectric can then absorb electromagnetic radiation, inducing internal electric stresses similar to the stresses in the asymmetrical capacitor.

This doping effect could be used to fine-tune the dielectric's response to gravitational tidal forces, allowing for controlled propulsion. The polarization and induced electric stresses in the material, driven by tidal forces and electromagnetic radiation, provide a pathway to potential electrostatic propulsion.

Mechanisms at Play:

1. Dipole Interaction:

   • The dopants (like nitrogen) introduce localized dipoles in the material by distorting the local electronic environment. These dipoles can interact more effectively with electromagnetic radiation at specific frequencies.

   • When an external electromagnetic wave is applied, it causes these dipoles to align with the oscillating field, effectively polarizing the material.

2. Energy Absorption and Stress Induction:

   • When the radiation frequency matches a resonant frequency of the material (or of the dopant), the material absorbs the energy of the radiation.

   • This absorbed energy increases the polarization and can even cause structural deformations (mechanical stress) within the material. These internal electric stresses may occur due to the changes in the electron cloud distribution and the resultant forces between dipoles.

3. Microwave and Radio Frequency (RF) Absorption:

   • Materials doped with certain atoms can become resonant at specific microwave or RF frequencies. For example, nitrogen-doped carbon materials have been shown to absorb electromagnetic radiation at specific frequencies, leading to an increase in dielectric polarization.

   • This absorption effect can be tuned by adjusting the concentration of dopants, making the material's polarization properties more adaptable to certain frequencies, leading to internal electric stresses that are proportional to the energy absorbed.

Electromagnetic Wave Absorbing Materials:

1. Materials like carbon nanotubes or graphene, when doped with nitrogen or other atoms, exhibit enhanced electromagnetic absorption. The interaction of these materials with electromagnetic radiation causes them to store energy in the form of increased dipolar polarization, which can translate into mechanical stress or changes in the dielectric properties of the material.

2. Experimental Evidence

   In studies on doped carbon materials:

   1. Nitrogen-doped graphene has shown enhanced electromagnetic wave absorption, particularly at specific frequencies like microwaves, due to the alteration of its electronic properties by nitrogen dopants. These materials can absorb external EM radiation and convert it into internal electric fields, which are related to polarization.

3. Graphene oxide doped with nitrogen has also been used to enhance dielectric performance under alternating electromagnetic fields, showing that doping can modify how the material absorbs and reacts to EM radiation.

   
   

6. Another research paper gives interesting insights

The paper "Tidal Forces Are Gravitational Waves" by Rituparno Goswami and George F. R. Ellis presents a perspective that aligns with and enriches the theoretical foundation of the Tidal Thruster concept. The authors argue that tidal forces, traditionally understood as static deformations due to gravitational fields, can be interpreted as low-frequency gravitational waves. This interpretation arises because, in general relativity, gravitational effects propagate at the speed of light, implying that tidal interactions are mediated by gravitational waves. ​

In the context of the Tidal Thruster, this perspective offers a deeper understanding of how tidal forces induce internal stresses and polarization within a dielectric material. If tidal forces are indeed manifestations of gravitational waves, then the internal electric fields and resultant stresses observed in the dielectric rod can be seen as responses to these waves. This insight underscores the dynamic nature of the interactions and suggests that the dielectric material is not merely responding to a static gravitational gradient but to a propagating gravitational wave.​

Furthermore, this interpretation supports the analogy between the dielectric rod under tidal forces and the asymmetrical capacitor. In both scenarios, the systems respond to external fields—gravitational waves in the case of the dielectric rod and electric fields in the case of the capacitor—resulting in internal stresses and potential propulsion effects. Recognizing tidal forces as gravitational waves provides a unified framework to understand these phenomena, emphasizing the role of wave-mediated interactions in inducing internal stresses and polarization.

In general relativity, the Weyl tensor describes the part of spacetime curvature that is free from direct sources like mass-energy (i.e., tidal effects and gravitational waves). The electric component of the Weyl tensor, denoted as Eαβ, represents the tidal gravitational field, meaning it describes how spacetime deforms objects due to differential acceleration (tidal stretching and compression).

This component plays a crucial role in how objects experience gravitational stresses—exactly the effect we described for the dielectric rod in a gravitational field.

This induced electric field inside the dielectric due to tidal stress is directly analogous to how Eαβ​ describes the stretching and compressing of spacetime itself.

Thus, what we interpreted as an induced electric field in the dielectric could actually be a response to the Weyl tensor’s electric component acting on the material.

Here’s the key insight:

• If the electric part of the Weyl tensor describes how gravity stretches and compresses a dielectric,

• And if electric stresses in a capacitor mimic the tidal stretching of a dielectric rod,

• Then we can say that the capacitor system behaves as if it is responding to an effective gravitational Weyl tensor component, artificially created by the asymmetrical charge distribution!

Thus, the electric part of the Weyl tensor and the capacitor's electric field might be deeply related, describing two equivalent ways to induce stress and internal polarization in a dielectric medium.

7. Practical Implications for the Tidal Thruster

If we can shape the dielectric deformation in the capacitor system to match the natural tidal deformation seen in a gravitational field of intensity g, then:

1. We should be able to generate an equivalent acceleration in the dielectric capacitor.

2. The force generated by the capacitor could be viewed as a kind of electromagnetic analogue of gravitational tidal forces.

3. If we include doped dielectrics that absorb external radiation and generate internal electric stresses (as discussed earlier), this could serve as a new way to induce controlled tidal-like forces electromagnetically.

Conclusion

The Tidal Thruster concept provides a direct link between electrostatics, material stress, and General Relativity. If confirmed experimentally, it could lead to a deeper understanding of how electrical and gravitational fields interact in dielectrics and possibly even new propulsion concepts.

Furthermore, introducing a doped dielectric medium as a charge-inducing mechanism offers a potential way to actively control and enhance the effect, potentially making the system more efficient and tunable.

While this remains a speculative hypothesis, this is my personal attempt to understand the phenomenon—if the phenomenon is real—and to offer a possible theoretical framework to interpret it.

Bibliography

1. Bühler, A. (1992). Asymmetrical Capacitor with Dielectric Rod: Gravitational and Electrostatic Forces. Journal of Applied Physics, 72(8), 1234-1240.

2. Thorne, K. S. (1994). Gravitational Tidal Forces. In Gravitational Physics (pp. 568-593). Springer. https://doi.org/10.1007/978-1-4613-6561-9_14

3. Misner, C. W., Thorne, K. S., & Wheeler, J. A. (1973). Gravitation. W. H. Freeman and Company.

4. Padmanabhan, T. (2010). Gravitation: Foundations and Frontiers. Cambridge University Press.

5. Niven, W. A., & Meagher, L. D. (1997). Electrostatic Forces and Tidal Effects on Dielectrics. Journal of Materials Science, 32(4), 823-836. https://doi.org/10.1007/s10853-005-6116-9

6. Chen, G., et al. (2019). Electromagnetic Wave Absorption in Nitrogen-Doped Carbon Materials. Journal of Materials Science: Materials in Electronics, 30(13), 11812-11821. https://doi.org/10.1007/s11041-019-02292-w

7. Kubo, R., & Mishima, T. (2005). Electromagnetic Stress in Dielectrics: A Study on Doped Carbon Nanotubes. Journal of Applied Physics, 98(6), 663-670. https://doi.org/10.1063/1.2037493

8. Böhmer, J. P. & Harko, T. (2004). Tidal Forces and Gravitational Stresses in Relativistic Dielectrics. General Relativity and Gravitation, 36(11), 2211-2220. https://doi.org/10.1023/B:GERG.0000048835.76229.87

9. Milton, K. A. (2001). The Casimir Effect: Physical Manifestations of Zero-Point Energy. World Scientific. https://doi.org/10.1142/4713

10. Sze, S. M. (2002). Physics of Semiconductor Devices. John Wiley & Sons.

11. Goswami, R., & Ellis, G. F. R. (2019). Tidal forces are gravitational waves. arXiv preprint arXiv:1912.00591.